参考:医学统计学 第16章第二节:Logistic回归 作者:李晓松 如有侵权立删其中的注解可以帮助理解前言:Logistic回归是一种十分常见的分类模型,是的严格来说这是一个分类模型,之所以叫做回归也是由于历史原因。
不同于线性回归中对于参数的推导,我们在这里运用的方式不再是最小二乘法,而是极大似然估计市面上Logistic回归大多都是在spss应用上,较少有针对其原理进行描述的本文参照医学统计学的书籍对Logistic回归做一个大概的描述,希望广大读者在使用Logistic回归时能够知其然也知其所以然。
下面开始这篇文章~多重线性回归模型要求因变量是连续型的正态分布变量,且自变量与因变量呈线性关系当因变量是分类变量,且自变量与因变量不呈线性关系时,就不能确足多重线性回归模型的适用条件此时,处理该类资料常用Logistic回归模型。
Logistic回归分析属于非线性回归,它是研究因变量为二项分类或多项分类结果与某些影响因素之间关系的一种多重回归分析方法在疾病的病因学研究中,经常需要分析疾病的发生与各危险因素之间的定量关系比如,研究食管癌的发生与吸烟、饮酒、不良饮食习惯等危险因素的关系。
如果采用多重线性回归分析,由于因变量y为二分类变量(通常取值0或1 ),不满足正态分布和方差齐等应用条件,若强行使用线性回归分析,其预测值可能会大于1或小于,而无法解释在流行病学研究中,虽然可以用Mantel-Haenszel分层分析方法分析多个因素的混杂作用,但这种经典方法有其局限性,随着混杂因素的增加,分层越来越细,致使每层内的数据越来越少,使相对危险度的估计产生困难。
Logistic回归模型较好地解决了上述问题,已经成为医学研究,特别是流行病学病因研究中最常用的分析方法之一注:Logistic回归可以算作是一种分类算法但也可以说是线性回归的拓展之所以还将其归于广义的线性回归是因为它的推导是利用化归的思想在试图构造一个线性模型来解释因变量。
视频学习可以参考:【机器学习】【白板推导系列】【合集 1~23】_哔哩哔哩 (゜-゜)つロ 干杯~-bilibiliwww.bilibili.com/video/BV1aE411o7qd?p=17

一、 Logistic回归分析的基本原理例:为探讨 μ\mu 阿片受体基因(OPRMI)中rsl3sl376和rs550014两个sNP位点与“首吸飘感”之间的关系,某研究调查了336名汉族海洛因依赖者,将海洛因依赖者分为有或无“首吸飘感”两组,同时收集每个个体的性别、年龄(岁)、首吸年龄(岁)等变量,数据见表16.6

由于因变量“首吸飘感”为二分类变量,本例应采用loglstic回归进行分析本节将以此为 例,说明loglstic回归分析的模型构建、分析步骤及实际应用等(一)Logistic回归模型参数的流行病学意义设因变量y是二分类变量,其取值为y=1(阳性结果:发病、有效、死亡等)或y=0(阴性结 果:未发病、无效、存活等),影响y取值的m个自变量分别为
x1,x2,……,xmx_{1},x_{2} ,……,x_{m} 例16.2中,因变量 y=1y=1 为具有首吸飘感, y=0y=0 为无首吸飘感;自变量分别为性别、年龄(岁)、首吸年龄(岁)、 rs1381376和rs550014两个SNP位点。
在 mm 个自变量(即暴露因素)作用下阳性结果发生的条件概率 p=p(y=1|x1,x2,……,xm)p=p(y=1|x_{1},x_{2} ,……,x_{m}) ,则Logistic回归模型可表示为:
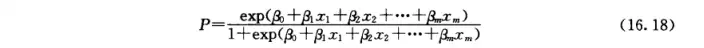
式子中: β0\beta_{0} 为常数项, 为偏回归系数β1,β2,...,βm为偏回归系数\beta_{1},\beta_{2},...,\beta_{m}为偏回归系数注:这个模型是与sigmiod函数关系密切,之所以选择这个函数一个非常重要的原因是因为概率值是在0-1之间的。
公式:公式:f(x)=11+e−x公式:f(x)=\frac{1}{1+e^{-x}}
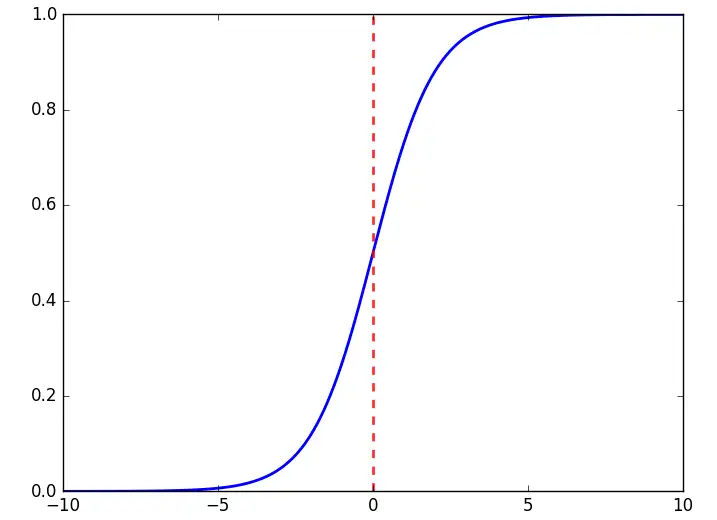
图像对式子进行logit变换,即 logit(p)=lnp1−plogit(p)=ln\frac{p}{1-p} ,即logistic回归模型可以表示成如下的线性形式:lnp1−p=β0+β1x1,β2
x2...,βmxmln\frac{p}{1-p}=\beta_{0}+\beta_{1}x_{1},\beta_{2}x_{2}...,\beta_{m}x_{m} (16.19)
注:这里就很好的讲问题化归为线性回归的问题而所谓logit变换,就是通过对pp进行变换之后再次纳入回归模型,得到的模型即为“Logistic回归模型”: 通过logit变换之后,就可将 0≤p≤10\leq p \leq1。
的资料转换为 −∞≤logit(p)≤+∞-\infty \leq logit(p) \leq +\infty 的资料由式子16.19可见,常数项 β0\beta_{0} 是当各种暴露因素均为0时,个体发病与不发病概率之比的自 然对数值。
偏回归系数 βj(j=1,2,...,m)\beta_{j}(j=1,2,...,m) 表示在其他自变量固定的条件下,第j个自变量每改变一个单位时 logit(p)logit(p) 的平均改变量它与比数比OR有对应关系。
在其他影响因素相同的情况下,某危险因素 xjx_{j} 的两个不同暴露水平 和c1和c0c_{1}和c_{0} 发病优势比的自然对数为:
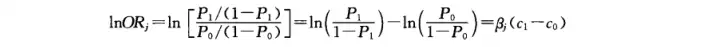
所以:

注:关于OR值,我们在使用的时候只需要理解OR值越大,阳性结果可能性就越大拿肺癌和吸烟之间的关系举例: 肺癌人群中吸烟不吸烟非肺癌人群中吸烟不吸烟肺癌人群中吸烟/不吸烟非肺癌人群中吸烟/不吸烟=OR\frac{肺癌人群中 吸烟/不吸烟}{非肺癌人群中 吸烟/不吸烟}=OR
,显而易见的 1">OR>1OR>1 ,则代表吸烟会加重得肺癌得概率(二)Logistic回归模型的分类根据因变量为二分类或多分类,logistic回归可相应的分为二分类logistic回归和多分类 logistic回归。
因变量为二分类变量时,根据设计类型的不同,可分别采用非条件logistic回归或条件logistic回归模型进行分析非条件logistic回归分析可用于成组设计的病例对照研究或队 列研究资料,条件logistic回归分析用于配对或配比设计的病例对照研究资料。
因变量为多项分类资料时,可用多项分类logistic回归模型进行分析本节所介绍的是其中的非条件logistic回归模型二、 Logistic回归分析的步骤(一)变量赋值及偏回归系数的意义logistic回归分析对自变量的要求并不严格,它可以是二分类变量、无序分类变量、有序分 类变量或定量变量.但对自变量需进行合理赋值。
对同一资料,变量采用不同的赋值方法,参数 的估计值、符号及含义都可能发生变化因此,变量赋值合理与否,直接影响着logistic回归的效果1、自变量的赋值二分类变量的赋值 习惯上把不暴露于某因素定为
x=0x=0 暴露于某因素定为 x=1x=1 ,回归模型为 logit(p)=β0+β1xlogit(p)=\beta_{0}+\beta_{1}x ,则对非暴露组有 logit(p)=β0+β1×0logit(p)=\beta_{0}+\beta_{1}\times0
,暴露组有 logit(p)=β0+β1×1logit(p)=\beta_{0}+\beta_{1}\times1 ,则暴露者与非暴露者的比数比 OR=eβ1OR=e^{\beta_{1}}无序多分类变量的赋值 对于无序多分类资料,比如职业、民族等,其数量化常用多个二分类(0 , 1)哑变量表示。
通常采用的赋值方法是假设某因素二分k类,则可用k一1个二分类变量表示,这时称每个二分类变量为哑变量.例如,职业〔包括教师、工人、农民三类职业),可用 x1,x2x_{1},x_{2}表示:其中 (x1,
x2)=(1,0)(x_{1},x_{2})=(1,0) 表示教师 (x1,x2)=(0,1)(x_{1},x_{2})=(0,1) 表示工人, (x1,x2)=(1,1)(x_{1},x_{2})=(1,1)
表示农民则仅有职业一个自变量的logistlc回归模型为 logit(p)=β0+β1x1+β2x2logit(p)=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2} ,职业为农民时
logit(p)=β0logit(p)=\beta_{0} ,教师的 logit(p)=β0+β1x1logit(p)=\beta_{0}+\beta_{1}x_{1} ,工人的 logit(p)=β0
+β2x2logit(p)=\beta_{0}+\beta_{2}x_{2} 因此,教师与农民相比的 ,OR=eβ1,OR=e^{\beta_{1}}, 工人与农民相比的 OR=eβ2OR=e^{\beta_{2}}。
;而教师与工人相比的 OR=eβ1−β2OR=e^{\beta_{1} - \beta_{2}}有序多分类变量的赋值方法 可分两种情况:①分组线性变量:若等级与 logit(p)logit(p) 呈线性关系,则以一个k等级变量赋值
0,1,2,...,k−10,1,2,...,k-1进入模型,此时 eβje^{\beta_{j}} 的含义是在其他自变量固定不变的前提下,自变量 xjx_{j} 每变动一个等级时的OR值 ②哑变量:若等级与 。
logit(p)logit(p) 不呈线性关系则按无序多分类变量的赋值方法表示,模型中的 eβje^{\beta_{j}} 意义同前述的无序多分类变量定量变量的赋值分为以下几种情况:①线性变量: 当自变量与 。
logit(p)logit(p) 呈线性关系时可将自变量以数值的形式直接纳人模型,此时 eβje^{\beta_{j}} 的含义是在其他自变量固定不变的前提下,自变量 xjx_{j} 每变动一个单位时的
OROR 值 ②二次或多次项变量:当自变量与 logit(p)logit(p) 呈曲线关系时,可以将自变量取二次或多次方比如,假设年龄 xx 与 logit(p)logit(p) 呈抛物线关系,则可拟合模型 。
logit(p)=β0+β1x+β2x2logit(p)=\beta_{0}+\beta_{1}x+\beta_{2}x^{2} ③ 分组线性变量:将自变量等级化后纳人模型,适用于将自变量等级化后与 。
logit(p)logit(p) 呈线性关系的情形比如,可将年龄分组为<10岁、 10岁~ 20岁~和30岁以上等,按分组线性变量纳人模型,这时模型为 logit(p)=β0+β1xlogit(p)=\beta_{0}+\beta_{1}x。
④哑变量:将定量变量分组等级化后,若与 logit(p)logit(p) 不呈线性关系,则按无序多分类资料的赋值方法表示,其模型构建同上述无序多分类变量2、因变量的赋值因变量赋值同分类变量赋值方法,一般“阳性反应”的赋值为1 , “阴性反应”的赋值为0。
如果因变量y赋值的顺序相反,则回归系数绝对值不变,但符号相反例如,对例16.2中的各变量的赋值情况见表16.7

(二)参数估计1.偏回归系数的估计常采用极大似然估计,其样本似然函数为:
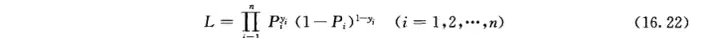
注:关于什么是极大似然估计,可以这样理解,目前已经发生的结果认定为这就是应该出现的结果,为什么会出现,因为出现这样的概率是最大那么我们就构造出发生这个事件的概率,求其最大值下的参数θ\theta而不同样本之间我们认为是相互独立的,所以他们的联合概率就是每一个样本概率的乘积。
2.OR的估计 当样本含量 nn 较大时, βj\beta_{j} 的抽样分布近似服从正态分布,若 xjx_{j} 只有暴露和非暴露2个水平,则比数比 ORjOR_{j} 的 100(1−α)100(1-\alpha)
%置信区间为
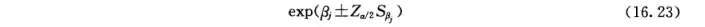
式中, SβjS_{\beta_{j}} 为 βj\beta_{j} 的标准误根据上述原理,例16.2的参数估计及假设检验结果见表16.8 表16.8显示了在调整了性别、年龄、首吸年龄的混杂作用后,rsl381376和rs550014两个sNP位点与“首吸飘感”的关联性。
其logistic回归模型可写为(其中,rsa表示rsl381376 , rsb表示rs550014).
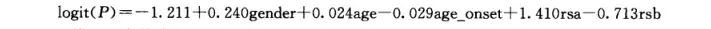
此模型及参数估计结果还需进一步做假设检验。
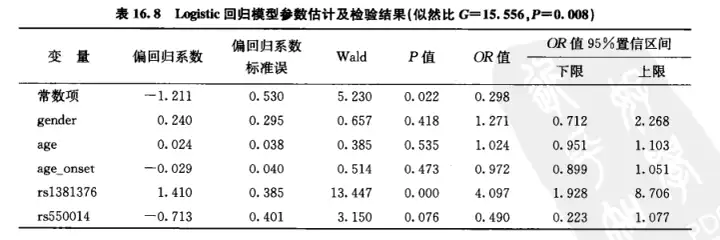
(三)模型的假设检验logistic回归模型的假设检验也包括检验摸型和检验模型参数两个方面。



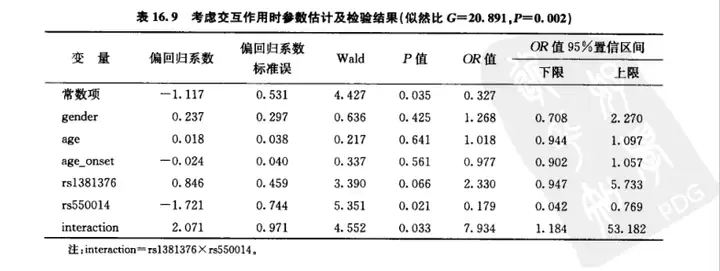
三、 Logistic回归分析的用途及应用条件(一)用途Logistic回归分析的主要用途有:建立用多个危险因素估计某事件(或疾病)在一定时期内发生概率的Logistic回归方程,如用于探索某疾病发生的危险因素并分析其作用大小。
测疾病或事件发生的概率比如在例16.2中,若某观察者的性别为女性,年龄为31岁,首吸年龄为29岁,rs381376位点发生突变,rs55ool4位点未发生突变,则根据表16.9中的参数估计结果,建立式(16.18)所示的Logistic回归模型,将该观察者的各变量取值代人模型,可得其发生“首吸飘感”的概率为0.402。
对样本进行判别归类。(二)应用条件Logistic回归分析的应用条件有:因变量为二项分类或多项分类资料。自变量可以是任意类型的资料,如定量资料、二分类资料、无序多分类资料或者有序分类资料等。

 sdf
sdf