logistics regression详解为了确定两种或两种以上变量间相互依赖的定量关系,参数及非参数检验都不好使这里就要用到回归分析除了资料相互之间进行比较的统计学方法外,临床研究中还存在另外一种情况:研究两组资料之间是否相互联系。
先看一个具体例子:
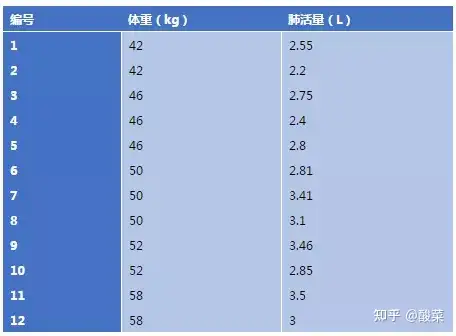
12名大一女生的体重与肺活量这里,如果我们想要研究肺活量是否随体重变化而变化,就要用到统计学上一种重要的统计方法:回归分析先看一个简单的方程式:ŷ=a+bx怎么样?像不像初中学的最简单的一元一次一次方程?其实,这就是最简单的一次函数。
只是统计学家们给它起了个高大上的名字:线性回归方程如果将两个事物的取值分别定义为变量x和y,x为自变量,y为因变量,即y因为x的变化而变化在上面这个例子中,体重就是x,而肺活量就是y一般而言,回归分析的数据需要满足以下四个条件:。
1. 线性趋势:x和y的关系是线性的如果不是,则不能进行线性回归分析;2. 独立性:因变量y的取值相互独立,它们之间没有联系;3. 正态性:因变量y的取值呈正态分布;4. 方差齐性:因变量y的方差相同后两个条件其实没有这么重要。
一般的临床研究只是建立回归方程,探讨x和y的关系,后两个条件不用管它们那么如何判断x和y的关系是否是线性的呢?这就要用到另外一个重要的工具:散点图散点图就是数据(x,y)在直角坐标系上的分布图这其实也是初中代数的内容。

图1,图2和图3都有明显的线性关系只不过图1,图2是直线,图3是曲线而图4却杂乱无章,不成线性关系所以,判断x和y的关系是否是线性关系就是做散点图现在市面上很多统计学软件都可以做散点图和计算回归方程我们只要输入一系列x值和y值。
结果会输出a值和b值,形成一个回归方程在回归方程ŷ=a+bx中,如果b﹥0,则y随着x的增大而增大,反映在散点图上,就是一条斜向上的直线,如图1所示;如果b﹤0,则y随着x的增大而减小,反映在散点图上,就是一条斜向下的直线,如图2所示。
而∣b∣越大,y随x的变化越大,反映在散点图上,直线越陡峭另外,回归方程还可以揭示变量x对变量y的影响大小,可以由回归方程进行预测和控制即根据一个特定的x值,就可以计算出一个特定的y值多元线性回归分析在上面所举例子,自变量和因变量都只有1个,如果自变量多于1个的情况下怎么办?
还是回到上面那个例子,但是增加了一组自变量——身高,即现在我们12名一年级女大学生体重,身高与肺活量的数据(见下图)。
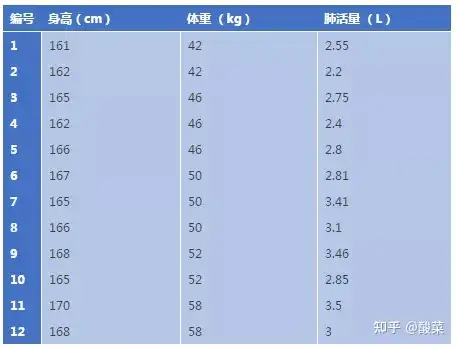
12名大一女生的体重,身高与肺活量如果我们想要研究肺活量是否随体重和身高变化而变化?体重和身高,哪个指标对肺活量的影响更大?这里就要用到统计学上另一种重要的统计方法:多元线性回归分析多元线性回归分析就是
研究一个因变量(这里是:肺活量)和多个自变量(这里是:体重和身高)之间的关系和一元线性回归方程差不多,多元线性回归方程只是增加了自变量而已:ŷ=a+b1x1+ b2x2x1和x2为两个自变量,y为因变量。
在上面这个例子中,身高是x1;体重是x2;而肺活量就是y如果通过计算,得出a=-0.5657;b1=0.005017;b2= 0.05406那么这个方程就可以写作:ŷ=-0.5657+0.005017x1+0.05406x2。
此方程表示:在x2,即体重,不变的情况下,身高每增加1cm,肺活量增加0.005017L多元线性回归方程同样可以进行对数据的预测和预报例如x1 =166,x2=46,代入公式,就可以得出ŷ=2.75这表示:身高为166 cm,体重为46公斤的一年级女大学生,预估的平均肺活量为2.75 L。
至此,问题就变得简单了,我们只需要算出a和b即可得到方程式。而现在的大部分统计学软件都可以做多元线性回归分析了,其输出的结果如下图所示:

要注意的就是红圈标注的三个数字,它们就是a,b1和b2另外,如果要判断几个自变量谁对因变量的影响更大,就看的标准系数就是图中蓝圈标注的二个数字在这里,显然身高对肺活量的影响更大另外,在多元线性回归中还存在一个自变量选择的问题。
这是因为不是所有的自变量都与因变量符合线性关系例如,我们在上一个例子中再引入一组血压的数据,这个血压就很有可能和肺活量完全风马牛不相及自变量选择的方法有前进法,后退法和逐步法一般采用逐步法就可以取得满意的结果,其输出的结果会自动告诉你哪些自变量被包括了,哪些自变量被排除了。
Logistic回归分析在临床研究中,很少出现上面这两种简单的情况,回归分析更多的是为了找到危险因素比如,为了研究老年患者颅脑手术后发生死亡的危险因素,研究人员总结出了以下几个可能的危险因素:年龄、肿瘤的性质、高血压、心功能不全、糖尿病。
那么,在这些可能的危险因素里面,哪些是真正有危险的?并且,哪种危险因素的危险性最高呢?这里要注意到的是:与上两个例子不同的是,这里的数据都是分类变量因变量的取值仅有两个:死亡与生存自变量的取值也仅有两个:如肿瘤的良性与恶性,高血压的有与无。
这时候,就要用到另外一种重要的回归分析方法:Logistic回归分析Logistic回归是一种概率分析,即分析当暴露因素为x时,个体发生某事件(y)的概率的大小Logistic的方程式为y=β0+β1X1+β2X2+…βmXm。
怎么样?看着眼熟吧?β1,β2…βm称为回归系数,反映了在其他变量固定后,x=1与x=0相比发生y事件的概率

记住OR越大,发生结果的可能性越大因为这类资料是分类资料,所以在做Logistic回归分析之前的第一件事就是赋值顾名思义,就是把分类资料赋予一定的数值一般赋予0或者1的数值阴性或者较轻的情况赋予0;阳性或者较重的情况赋予1。
如下表所示
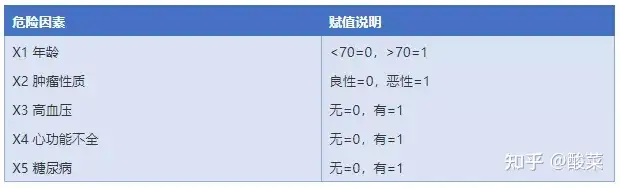
赋值完成之后,就可以正式开始Logistic回归分析了,一般而言,其分析结果如下图所示。
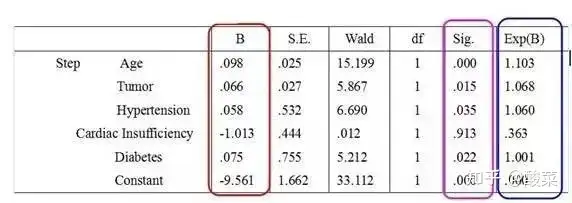
红圈标注的数字,就是Logistic的方程式中的β0和回归系数把相应的数字代入方程式,就可以得出Logistic回归方程式:y=-9.561+0.098X1+0.066X2+0.058X3-1.013X4+0.075X5。
那么,如何判断在这些可能的危险因素里面,哪些是真正有危险的?这就需要看紫圈标注的数字,如果p﹤0.05,就认为是真正的危险因素;如果p﹥0.05,就认为不是危险因素由图可知,在这个例子里,唯一的非危险因素就是心功能不全(Cardiac Insufficiency)。
另外,如何判断哪种危险因素的危险性最高呢?那就要看蓝圈标注的最后一列数字这列数字其实就是OR数值越大,表明发生结果的概率越大由图可知,在这个例子里面,年龄的危险性最高另外,Logistic回归分析对样本量是有一定要求的。
这里有个简单的估算方法:样本量为自变量个数的10倍在本文的例子中,有5个自变量,那么就要有至少50位患者的数据,才能进行Logistic回归分析必须注意到的是:Logistic回归分析要求应变量为分类变量(如本文例子中的生存/死亡)。
但是,自变量并不一定非要是分类变量它们也可以是连续变量和离散变量本文的例子中采用了分类变量,只是为了方便举例至于logistic回归分析的具体实现方法,《医学研究中的logistic回归分析及SAS实现》一书中则讲解十分细致,通过各种实例对logistic回归的分析过程进行了深入探讨,对logistic回归应用中经常遇到的各种问题分别作了深入浅出的阐述。

本书不仅介绍了logistic回归在不同设计方法中的应用,而且引入了近几年与logistic回归相关的一些新的方法的介绍,使读者能够在不同的应用场合找到相应的分析方法。

本书侧重于阐述统计分析的思路,而非一味枯讲理论,同时辅以SAS软件操作的具体过程和应用范例,符合广大科研人员的需求,可让读者从中学到logistic回归的分析思路以及比较实用SAS语句,而且能解决大多数的临床科研论文写作过程中的统计学问题。

如今免费送书在即,限量300本,你还不快快行动么?扫描下方海报中的二维码,即可免费领取此书哦!

 sdf
sdf